CNN学习笔记-批正则化(Batch Normalization)
批标准化(Batch Normalization)
解决Internal Covariate Shift问题
IID:独立同分布(independently identically distribution),指的是随机变量服从同一分布,并且互相独立,那么这些随机变量是独立同分布。
然而网络层数的增加,每一层的输入分布就会改变,从而不符合IID假设,网络也很难学习到稳定的科学规律,因为每一层针对的都是新的数据分布,只能通过很小的学习速率和精调的初始化参数来解决这个问题。
由于现在的CNN通常包含很多的隐藏层,在训练过程中每一层的分布都会发现变化,因此CNN中的每一层网络都会发生协变量偏移(Covariate Shift)问题。由于是对中间隐藏层的分析,所以叫做内部协变量偏移(Internal Covariate Shift)。
为了使每一层的输入分布固定下来,提出了Batch Normalization。
核心思想
在深度神经网络训练过程中使得每一层神经网络的输入保持相同分布的,可以解决随着网络深度加深,训练起来越困难,收敛越来越慢的问题(relu激活函数,resnet都是用来解决这个问题的)
BN是有启发来源的:之前的研究表明如果在图像处理中对输入图像进行白化(Whiten)操作的话——所谓白化,就是对输入数据分布变换到0均值,单位方差的正态分布——那么神经网络会较快收敛,那么BN作者就开始推论了:图像是深度神经网络的输入层,做白化能加快收敛,那么其实对于深度网络来说,其中某个隐层的神经元是下一层的输入,其实深度神经网络的每一个隐层都是输入层,不过是相对下一层来说而已,那么就可以对每个隐层都做白化。BN就可以理解为对深层神经网络每个隐层神经元的激活值做简化版本的白化操作。
如人们以前常用的sigmod激活函数,可以看出两端的导数值接近于0,所以当分布偏移至两端时,就会发现梯度消失的现象。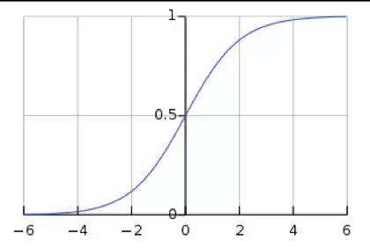
BN的基本思想其实相当直观:因为深层神经网络在做非线性变换前的激活输入值。随着网络深度加深或者在训练过程中,其分布逐渐发生偏移或者变动,之所以训练收敛慢,一般是整体分布逐渐往非线性函数的取值区间的上下限两端靠近,导数接近于0,所以这导致反向传播时低层神经网络的梯度消失,这是训练深层神经网络收敛越来越慢的本质原因,而BN就是通过一定的规范化手段,把每层神经网络任意神经元这个输入值的分布强行拉回到均值为0方差为1的标准正态分布,其实就是把越来越偏的分布强制拉回比较标准的分布,这样使得激活输入值落在非线性函数对输入比较敏感的区域,这样输入的小变化就会导致损失函数较大的变化,梯度变大就避免梯度消失问题产生,而且梯度变大意味着学习收敛速度快,能大大加快训练速度。
整个过程可以用下图表示: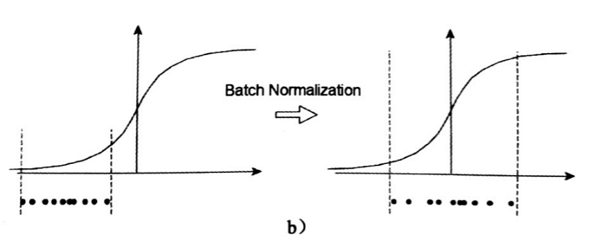
每一层的输入数据先经过BN操作后,再传入激活函数中(Activation function)。
训练细节
Batch Normalization是基于Mini-Batch的。
步骤3中\(\epsilon\)的作用是:避免方差为0引入的微小正数。
步骤4中的两个参数\(\gamma\)和\(\beta\)为scale和shift,分别代表缩放和偏移。
为何要有步骤4:
BN得到的正态分布未必是最能体现样本特征的分布,会在一定程度上削弱网络的表达能力。若\(\gamma\)和\(\beta\)初始化为\(\mu_B\)和\(\sigma_B\)时,数据就会从正态分布还原成原始分布。加上这两个系数后,使得正态分布从正中心像两边调整些,在标准正态分布和原始分布之间找到一个平衡,从而最能体现数据的分布规律。
scale和shift是通过训练学习得到的,有一定的自适应性,增强了网络的表达能力。
同时在进行了BN操作的层中不需要bias偏置量了,因为在对数据进行BN后,bias的作用会被抵消,平移的功能交给β来实现。
整个训练过程的可视化如下图:
BN层种通常有三个系数:均值(mean)、方差(variance)、滑动平均衰减系数(moving average factor,通常取接近于1的数)
BN作用于:
- 全连接层,对Mini-Batch内的每个结点求均值和方差。
- 卷积层,对feature map每一个结点的channel纬度做BN操作。
预测细节
在训练阶段中,我们可以对每个Mini-Batch求出均值和方差,作为BN调整的方向。
但在进行预测阶段时,预测实例只有一个,自然无法求出他的均值和方差。
为了解决这个问题,对于训练集中的每个Mini-Batch,记录下他的均值和方差。对所有Mini-Batch求得的均值和方差求数学期望,把这两个全局统计量作为预测阶段的scale和shift。
计算过程如下:
$$
E[x]\leftarrow E_B[\mu_B]
\\
Var[x]\leftarrow \frac{m}{m-1} E_B[\sigma_B^2]
$$
在最后预测阶段,使用的公式为:(在预测阶段中,每一层的\(\gamma\)和\(\beta\)已经确定)
$$
y = \gamma \frac{x-E(x)}{\sqrt{Var(x) + \epsilon}} + \beta= \frac{\gamma}{\sqrt{Var(x) + \epsilon}} x + ( \beta - \frac{\gamma E(x)}{\sqrt{Var(x) + \epsilon}} )
$$
然而在实际操作过程中,通常使用指数滑动平均(ExponentialMovingAverage,EMA)的方法代替求平均值。这是因为在所有Mini-Batch中求得的平均值,刚开始求的数据与最后训练完求得数据相差较大,单纯求平均值误差较大。
优点
- 避免了梯度消失的问题,不仅仅极大提升了训练速度,也使得收敛过程大大加快;
- 增加正则化效果,由于是在Mini-Batch上而不是在整个数据集上计算均值和方差,并且在经过scale和shift会引入少许噪声,类似于Dropout减少神经元之类的依赖关系,可以看作是一种正则化手段,所以不用Dropout也能达到相当的效果;
- 调参过程也简单多了,对于初始化要求没那么高,而且可以使用大的学习率等。
引用
[1]Ioffe S , Szegedy C . Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift[J]. 2015.
